LAN-tastic Triangles

When people ask why I disappear every December to work on my Advent of Code solution, my answer is simple:

• It’s incredibly fun.
• I learn so much along the way.

This is especially true for days like this where solving the problem doesn’t require reinventing the wheel, but instead relies on understanding how it’s been solved before.

Today's input consists of a list of connections between computers - essentially a network map:

kh-tc
de-co
qp-kh
de-cg
ka-co
yn-aq
de-ta
qp-ub
cg-tb
ta-co
ta-ka
...

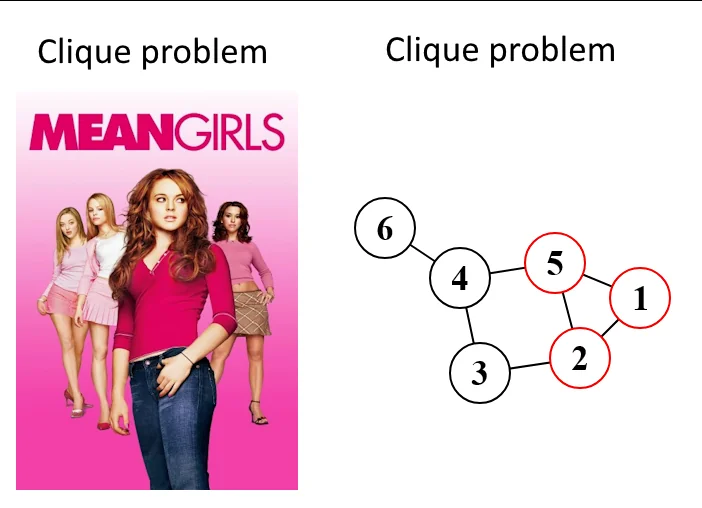
The goal for now is to find sets of three inter-connected computers (i.e. where each computer is connected to the other two). For instance, in the portion of input above we can observe a couple:

co,ka,ta
de,ka,ta

In particular, the answer is to find a subset of such triplets - specifically, all triplets having at least one computer whose name starts with t - but let's worry about this in due time.

So, my first function to solve part 1 is to create an adjacency list: for every pair of computers, I want to stores all computers connected to each member of the pair

function getAdjacencyList(lines: string[]) {
    const adjacencyList: { [key: string]: Set<string> } = {};
    for (const connection of lines) {
        const [a, b] = connection.split('-');
        if (!adjacencyList[a]) adjacencyList[a] = new Set();
        if (!adjacencyList[b]) adjacencyList[b] = new Set();

        adjacencyList[a].add(b);
        adjacencyList[b].add(a);
    }
    return adjacencyList;
}

After running this, we get a list where each item is linked to a list of all connected nodes from our input. For example:

kh: [tc, qp, ub, ta]
tc: [kh, wh, td, co]
...

From our adjacency list, we can proceed to identifying a "triangle" (fundamentally a cycle of three connected nodes) of computers: for each node, the function checks pairs of its neighbors to see if they are also connected, i.e. forming a triangle. It then stores each found triangle as a sorted, comma-separated string in a Set, to ensure we don't consider the same triangle twice.

const triangles: Set<string> = new Set();
for (const [node, neighbors] of Object.entries(adjacencyList)) {
    const neighborsArray = Array.from(neighbors);

    for (let i = 0; i < neighborsArray.length; i++) {
        for (let j = i + 1; j < neighborsArray.length; j++) {
            const neighborA = neighborsArray[i];
            const neighborB = neighborsArray[j];

            if (adjacencyList[neighborA].has(neighborB)) {
                const triangle = [node, neighborA, neighborB].sort().join(',');
                triangles.add(triangle);
            }
        }
    }
}

The last bit is to count all triangles having at least one computer name starting with T, which can be done easily:

let trianglesStartingWithT = 0;
[...triangles].forEach((triangle: string) => {
    const split = triangle.split(',');
    if (split.some((s) => s.startsWith('t'))) {
        trianglesStartingWithT++;
    }
});

return trianglesStartingWithT;

Understandably, to solve part 2 we need to find the largest set of computers that are all connected to each other. Sounds trivial, doesn't it? 😛

Well, I'm not going to annoy you with the summary of my failed attempts at solving this "my way", because it took way too long, and frankly I don't even remember the process with too much detail at this stage 😅

Let's just say, after some research I bumped into the Bron-Kerbosch algorithm, that seems to be just perfect for what we need here!

Essentially, my input features ~3400 connections, so generating all possible subsets is computationally infeasible because of exponential complexity. However, Bron-Kerbosch comes in handy, since it is designed for finding all maximal cliques (that is our largest set of connected computers) within a graph in an efficient way.

If you never heard of this algorithm, you're in good company. Here's the clearest explanation I managed to find of what the various steps are - for the benefit of the reader but especially mine:

It operates on three sets:

• R (Current Clique): Nodes included in the current clique.
• P (Candidates): Nodes that can be added to the current clique.
• X (Excluded): Nodes already considered and excluded from the current clique.

At each step:

• If P and X are empty, R is a maximal clique.
• A pivot is selected to reduce the search space and optimize performance. Recursive calls refine these sets to explore possible cliques.

After figuring out how to translate this beauty into runnable code, I came up with this:

const findLargestParties = (adjacencyList: { [key: string]: Set<string> }) => {
    const parties: string[][] = [];

    const bronKerbosch = (r: Set<string>, p: Set<string>, x: Set<string>) => {
        if (p.size === 0 && x.size === 0) {
            parties.push([...r]);
            return;
        }

        const pivot = p.size > 0 ? [...p][0] : null;
        const pivotNeighbors = pivot ? adjacencyList[pivot] : new Set();

        for (const node of [...p].filter((n) => !pivotNeighbors.has(n))) {
            bronKerbosch(
                new Set([...r, node]),
                new Set([...p].filter((n) => adjacencyList[node].has(n))),
                new Set([...x].filter((n) => adjacencyList[node].has(n)))
            );
            p.delete(node);
            x.add(node);
        }
    };

    bronKerbosch(new Set(), new Set(Object.keys(adjacencyList)), new Set());
    return parties;
};

Running this on our adjacency list (computed for part 1), the result is an array of arrays, each containing the cliques of interconnected computers.

[
 [de, cg],
 [de, ka, co, ta],
 [cg, yn, aq],
 [aq, vc, wq],
 ...
]

Finding the largest list in the group is then easy - I simply used reduce for the purpose:

const findLargestParty = (parties: string[][]) => {
    return parties.reduce(
        (max, party) => (party.length > max.length ? party : max),
        []
    );
};

Et voila, the computers have been sorted, a new algorithm has been learned, and two brand new, precious stars are now in my bag 🤩